Tips on how to use this exercise at home and at school.
Early math concepts
The child already understands the problem when the instruction corresponds to the solution ("there should be 1 more picture in the blue box than in the red box", so he adds more pictures to meet the condition). Now they are required to understand the same situation, but the assignment conditions change. One group is "locked", so the child must use existing knowledge. If they can't add to the blue box, they must subtract the pictures in the red box. In this exercise, they work with several objects up to 10.
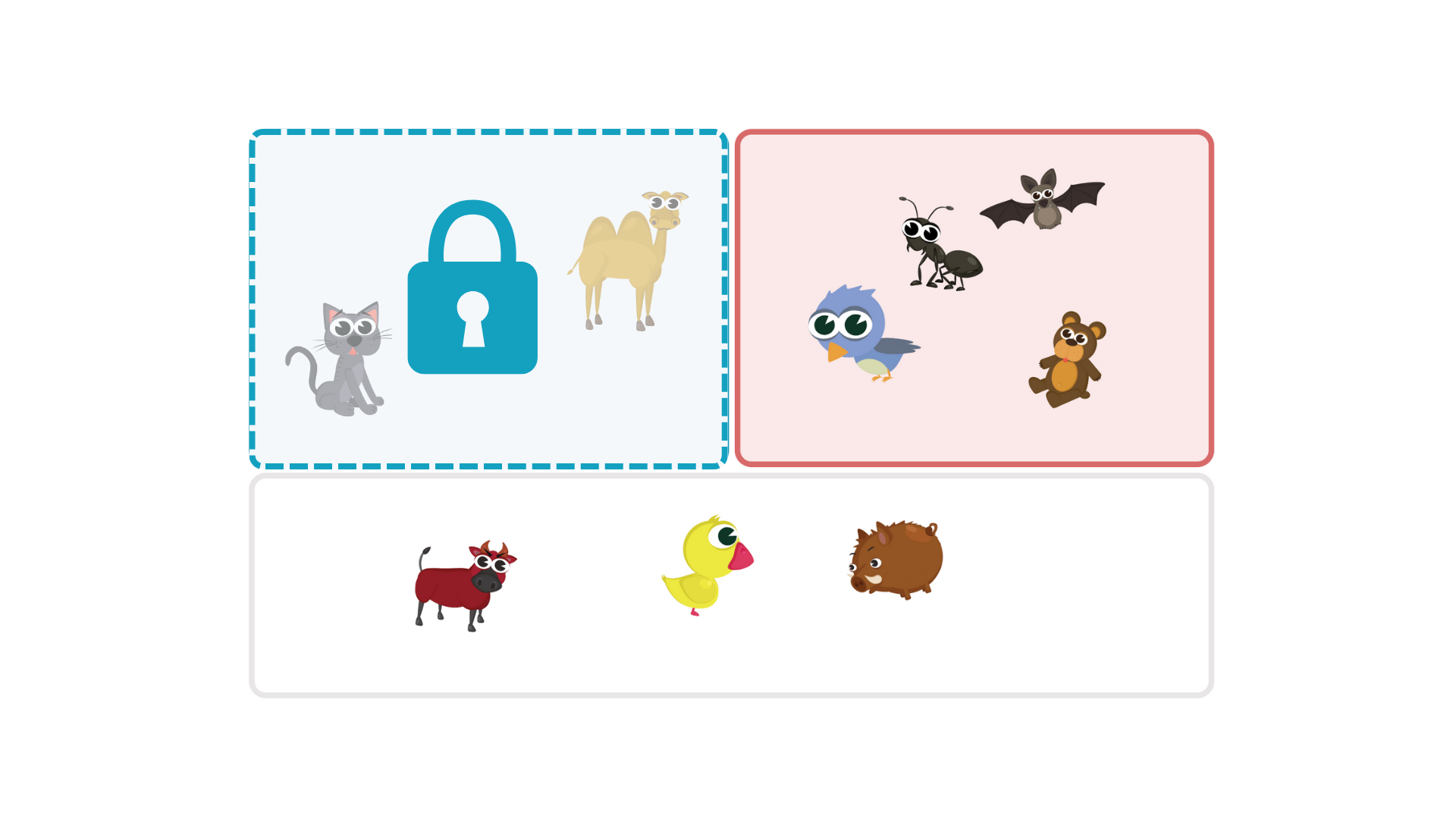
Why is this exercise important?
This exercise promotes a deep understanding of the principle of reversibility or its validation in diagnostics. The child is confronted with the need to understand a linguistic instruction which, however, does not correspond to the solution offered first. He must understand the problem. The child will encounter this later. For example, Adam has three candies, and that's one more than Dan. How many candies does Dan have? The child must resist the initial consideration think the problem through more and discover a possible solution by reverse operation.
Who is the exercise suitable for?
Generally belongs in preschool or early school play. In addition to the concepts of number ideas, and reasoning assumptions, it also develops language skills at the same time.
Methodological recommendations
We can only proceed with the exercise when we are sure that the child understands more about/less about relationships and can use them.
The child may not understand at the first moment that the task has changed and will perform the task regardless of the locked group. In that case, we allow them to listen to the instruction again.
Invite the child to think aloud. This makes it easier for the child to discover the apparent 'contradiction' between the instruction and the solution to the problem.
If the contradiction is not discovered on its own, we ask: How else could you have completed the task? How is it different?
Tips for similar activities outside the application
We can also practice the higher by and lower by relationships on the stairs: You are standing 2 steps higher than me. I would like you to stand 1 step lower than me. But you must not move. How do we solve the problem?
I'm 2 cubes taller than you. I want you to be 1 block higher. You can't move your building. So what do we do to make your building taller than mine?